• Explicit solution

Regulation problem

Finite horizon MPC

Online solution

Explicit solution

Finite horizon MPC with terminal penalty and terminal set constraints

Regulation to a nonzero steady state

• Online solution
• Explicit solution

As an example, let us consider an LTI prediction model, represented by the state-update equation {$x^+ = A x + B u$} with {$A = \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix}$} and {$ B = \begin{bmatrix} 1 \\ 0.5 \end{bmatrix} $}

• Add state constraints {$ \begin{bmatrix} -5 \\ -5 \end{bmatrix} \le x \le \begin{bmatrix} 5 \\ 5 \end{bmatrix} $}

• Add input constraints {$-1 \le u \le 1 $}:

• Add quadratic state penalty, i.e., penalize {$ x_k^T Q x_k $} with {$ Q = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} $}

• Use quadratic penalization of inputs, i.e., {$ u_k^T R u_k $} with {$ R=1 $}:

Finally, we can synthesize an MPC controller with prediction horizon say {$ N=5 $}:

As an example, let us consider an LTI prediction model, represented by the state-update equation x^+ = A x + B u with A = [1 1; 0 1] and B = [1; 0.5]:

model.u.penalty = QuadFunction(R);

• Regulation to a nonzero steady state

Regulation to a nonzero steady state

• Regulation to nonzero steady state

Regulation to nonzero steady state

The next example demonstrates how to achieve regulation to a nonzero steady state. Consider a model of an aircraft discretized with 0.2s sampling time

(:source lang=MATLAB -getcode:)

A = [0.99 0.01 0.18 -0.09 0; 0 0.94 0 0.29 0; 0 0.14 0.81 -0.9 0; 0 -0.2 0 0.95 0; 0 0.09 0 0 0.9];
B = [0.01  -0.02; -0.14 0; 0.05 -0.2; 0.02 0; -0.01 0];
C = [0 1 0 0 -1; 0 0 1 0 0; 0 0 0 1 0; 1 0 0 0 0];
model = LTISystem('A', A, 'B', B, 'C', C, 'Ts', 0.2); 

Given the dynamics of the model, one can compute the new steady state values for a particular value of the input, e.g.

(:source lang=MATLAB -getcode:)

us = [0.8; -0.3];
ys = C*( (eye(5)-A)\B*us );

The computed values will be used as references for the desired steady state which can be added using "reference" filter

(:source lang=MATLAB -getcode:)

model.u.with('reference');
model.u.reference = us;
model.y.with('reference');
model.y.reference = ys;

To fomulate MPC optimization problem one shall provide constraints and penalties on the system signals. In this example, only the input constraints are considered

(:source lang=MATLAB -getcode:)

model.u.min = [-5; -6];
model.u.max = [5; 6];

The penalties on outputs and inputs are provided as quadratic functions

(:source lang=MATLAB -getcode:)

model.u.penalty = QuadFunction( diag([3, 2]) );
model.y.penalty = QuadFunction( diag([10, 10, 10, 10]) );

which yields a quadratic optimization problem to be solved in MPC. The online MPC controller object is constructed with a horizon 6

(:source lang=MATLAB -getcode:)

ctrl = MPCController(model, 6)

and simulated for zero initial conditions over 30 samples

(:source lang=MATLAB -getcode:)

loop = ClosedLoop(ctrl, model);
x0 = [0; 0; 0; 0; 0];
Nsim = 30;
data = loop.simulate(x0, Nsim);

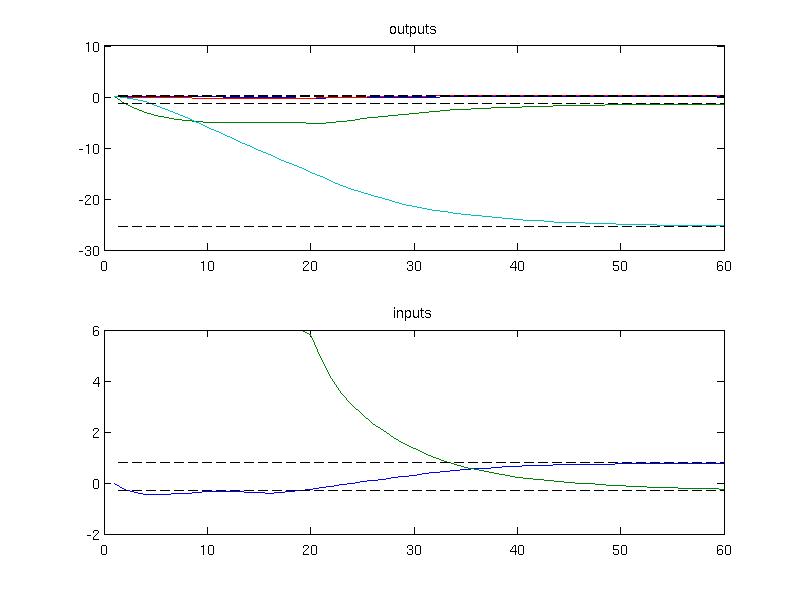
The simulation results can be plotted to inspect that the convergence to the new steady state has been achieved

(:source lang=MATLAB -getcode:)

subplot(2,1,1)
plot(1:Nsim, data.Y);
hold on;
plot(1:Nsim, ys*ones(1, Nsim), 'k--')
title('outputs')
subplot(2,1,2)
plot(1:Nsim, data.U);
hold on;
plot(1:Nsim, us*ones(1, Nsim), 'k--')
title('inputs')

• Finite horizon MPC
• Finite horizon MPC with terminal penalty and terminal set constraints

---

Finite horizon MPC

Finite horizon MPC with terminal penalty and terminal set constraints

@]

Back to MPC synthesis overview.

Regulation problem

To create an MPC controller in MPT3, use the MPCController constructor:

(:source lang=MATLAB -getcode:)

mpc = MPCController(sys)

where sys represents the prediction model, created by LTISystem, PWASystem or MLDSystem constructors (see here).

As an example, let use consider an LTI prediction model, represented by the state-update equation x^+ = A x + B u with A = [1 1; 0 1] and B = [1; 0.5]:

(:source lang=MATLAB -getcode:)

model = LTISystem('A', [1 1; 0 1], 'B', [1; 0.5]);

Next we specify more properties of the model:

• Add state constraints [-5; -5] <= x <= [5; 5]:

(:source lang=MATLAB -getcode:)

model.x.min = [-5; -5];
model.x.max = [5; 5];

• Add input constraints -1 <= u <= 1:

(:source lang=MATLAB -getcode:)

model.u.min = -1;
model.u.max = 1;

• Add quadratic state penalty, i.e., penalize x_k^T Q x_k with Q = [1 0; 0 1]:

(:source lang=MATLAB -getcode:)

Q = [1 0; 0 1];
model.x.penalty = QuadFunction(Q);

• Use quadratic penalization of inputs, i.e., u_k^T R u_k with R=1:

(:source lang=MATLAB -getcode:)

R = 1;
model.u.penalty = OneFunction(R);

A number of other constraints and penalties can be added using the concept of filters.

Finally, we can synthesize an MPC controller with prediction horizon say N=5:

(:source lang=MATLAB -getcode:)

N = 5;
mpc = MPCController(model, N)

Now the mpc object is ready to be used as an MPC controller. For instance, we can ask it for the optimal control input for a given value of the initial state:

(:source lang=MATLAB -getcode:)

x0 = [4; 0];
u = mpc.evaluate(x0)

u =

    -1

You can also retrieve the full open-loop predictions:

(:source lang=MATLAB -getcode:)

[u, feasible, openloop] = mpc.evaluate(x0)

openloop = 

    cost: 32.4898
       U: [-1 -1 0.1393 0.3361 -5.2042e-16]
       X: [2x6 double]
       Y: [0x5 double]

Please consult this page to learn how to perform closed-loop simulations in MPT3.

Once you are satisfied with the controller's performance, you can convert it to an explicit form by calling the toExplicit() method:

(:source lang=MATLAB -getcode:)

expmpc = mpc.toExplicit();

This will generate an instance of the EMPCController class, which represents all explicit MPC controllers in MPT3. Explicit controllers can be used for evaluation/simulation in exactly the same way, i.e.,

(:source lang=MATLAB -getcode:)

[u, feasible, openloop] = expmpc.evaluate(x0)

openloop = 

    cost: 32.4898
       U: [-1 -1 0.1393 0.3361 -5.2042e-16]
       X: [2x6 double]
       Y: [0x5 double]

h1. Adding terminal set and terminal penalty

Consider an oscillator model defined in 2D.

(:source lang=MATLAB -getcode:)

A = [ 0.5403, -0.8415; 0.8415,  0.5403];
B = [ -0.4597; 0.8415];
C = [1 0];
D = 0;

Linear discrete-time model with sample time 1

(:source lang=MATLAB -getcode:)

sys = ss(A,B,C,D,1);
model = LTISystem(sys);

Set constraints on output

(:source lang=MATLAB -getcode:)

model.y.min = -10;
model.y.max = 10;

Set constraints on input

(:source lang=MATLAB -getcode:)

model.u.min = -1;
model.u.max = 1;

Include weights on states/inputs

(:source lang=MATLAB -getcode:)

model.x.penalty = QuadFunction(eye(2));
model.u.penalty = QuadFunction(1);

Compute terminal set

(:source lang=MATLAB -getcode:)

Tset = model.LQRSet;

Compute terminal weight

(:source lang=MATLAB -getcode:)

PN = model.LQRPenalty;

Add terminal set and terminal penalty

(:source lang=MATLAB -getcode:)

model.x.with('terminalSet');
model.x.terminalSet = Tset;
model.x.with('terminalPenalty');
model.x.terminalPenalty = PN;

Formulate finite horizon MPC problem

(:source lang=MATLAB -getcode:)

ctrl = MPCController(model,5);