Geometry /

Unions

Objects for representation of unions of sets

The Union object - unions of general convex sets

The Union object is the high level class for representing unions of convex sets. The union can be comprised of any sets derived from the ConvexSet class, such as YSet and Polyhedron objects. To construct the Union object, it suffices to provide the sets concatenated in an array as an argument:

 P(1) = Polyhedron('lb', -1, 'ub', 1);
 P(2) = Polyhedron('lb', 1);
 U = Union(P)

The same applies for YSet objects

 x = sdpvar;
 S(1) = [ x <= -2 ];
 S(2) = [ -2 <= x <= 2 ];
 S(3) = [ x >= 2];
 U = Union(S)

To create union that combines Polyhedron and YSet objects, one can employ add method, for instance

 x = sdpvar(2,1);
 S = YSet(x, [ x(1) + x(2) <= 1; -2*x(2) + 0.5*x(1) >= 2.3 ]);
 P = Polyhedron('A', randn(4,3), 'b', rand(4,1));
 U = Union(S)
 U.add(P)

Note that the sets do not have to be in the same dimension. In the above example, the set "S" is in dimension 2 whereas the set "P" is in the dimension 3. Other sets can be added using the add method, e.g.

 U.add( Polyhedron('lb', 1, 'ub', 5) )

The set can be also removed from the union. This is achieved with remove method by referring to the index of the set to remove, e.g.

 U.remove(3)

It is possible to store arbitrary data with the Union object. The user data can be provided in the extended syntax at the time of construction, e.g.

 d.a = -2.5;
 d.b = 0.8;
 z = sdpvar(2,1);
 S(1) = YSet(z, [ cone(z(1),z(2)); 0 <= z <= 1]);
 S(2) = YSet(z, [ z(1)-2*z(2) <= 0.4; 0.1*z(2) <= 0.1]);
 U = Union('Set', S, 'Data', d)

or attached after creation of the object

 U.Data.c = 2.1;

There are three properties of the Union object:

  • Num - indicates the number of sets in the union
  • Set - stored sets of the union in a cell array
  • Data - place for storing arbitrary user data with the union

The properties can be accessed by referring to their names, i.g.

 U.Num
 U.Set
 U.Data

The Data property can be modified after the object has been created, other properties are not changeable. The properties are useful when extracting information about the union, for instance, consider the union of a box and a circle:

 box = Polyhedron('lb', [-2; -2], 'ub', [0; 0]);
 x = sdpvar(2,1);
 circle = YSet(x, [ norm(x-1, 2) < 3 ] );
 U = Union(box);
 U.add(circle)

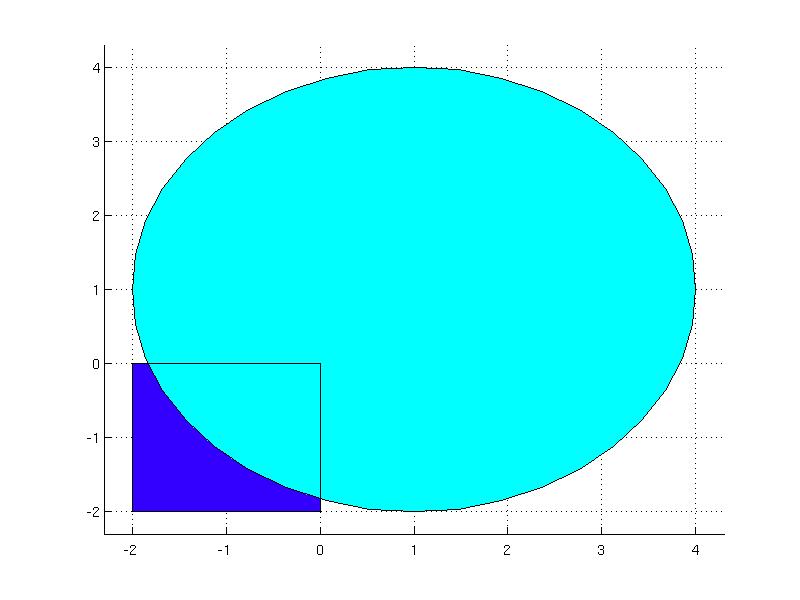
The total number of sets in the union is given by the property

 U.Num

and the individual sets can be acessed by index in the Set property in the order as they were stored

 B = U.Set(1)
 C = U.Set(2)

The PolyUnion object - unions of polyhedra

The PolyUnion objects represents unions of polyhedra in the same dimension. The dimension check is the only requirement for construction of PolyUnion objects. To construct a PolyUnion object an union one has to supply an array of polyhedra in the same dimension. In the next example it is shown how to construct an union of three intervals in dimension one:

 P(1) = Polyhedron( 'lb', -10, 'ub', -5);
 P(2) = Polyhedron( 'lb', -5, 'ub', 5);
 P(3) = Polyhedron( 'lb', 5, 'ub', 10);
 U = PolyUnion(P)

In this example an union of two polyhedra is constructed in dimension 2 - the first polyhedron is in V-representation and the second in H-representation:

 R = Polyhedron( [-1.0  -0.8;  -2.9  1.4;  0.3 -0.7; 1.3 -1.7;  -0.1 -0.2], [2.1; 3.4; 0.5; 5.1; 0.8]);
 S = Polyhedron( [-4.3  0.3;  -6.0 -5.5;  0.0  7.6; -3.8 1.8]);
 U = PolyUnion([R, S])

The dimension of the PolyUnion object can be retrieved from Dim property:

 U.Dim

other properties are inherited from the Union object:

  • Num - the number of polyhedra in the union,
  • Set - stored polyhedra in a polyhedron array,
  • Data - arbitrary user data stored.

The number of sets forming in the union can be read in Num property, i.e.

 U.Num

To access the individual sets from the PolyUnion object one can use the Set property, for instance the second polyhedron can be read by pointing to it with index 2:

 U.Set(2)

If other user data have been stored with the object, it can be accessed in Data property

 U.Data

Polyhedra can be added/removed from the PolyUnion object. To add new polyhedra to the union, the dimension must be retained and the added polyhedron must not be empty:

T = Polyhedron('A', [ 2.5 -0.6; 0.1 -0.08; -1.9 -0.4; 1.7  0.8], 'b', [5.5; 3.8; 4.9; 7.5], 'Ae', [ 0.5 -0.2], 'be', 1.2);
U.add(T)

Removing the polyhedron from the PolyUnion object is based on an index of the set which to remove, i.e.

U.remove(2)

For the usage in computational geometry it is of intereset to exploit the properties of the union of polyhedra, such as convexity and overlaps. If these properties are know at the time of the construction of the PolyUnion object, one can associate these properties directly to the union. The following properties can be attached to the PolyUnion object:

  • Convex - logical flag indicating if the union convex or not
  • Overlaps - logical flag indicating if the polyhedra in union overlap or not
  • FullDim - logical flag indicating if the union is build from just from full-dimensial polyhedra or not
  • Bounded - logical flag indicating if the union is build from just from bounded polyhedra or not
  • Connected - logical flag indicating if the union convex is connected or disconnected

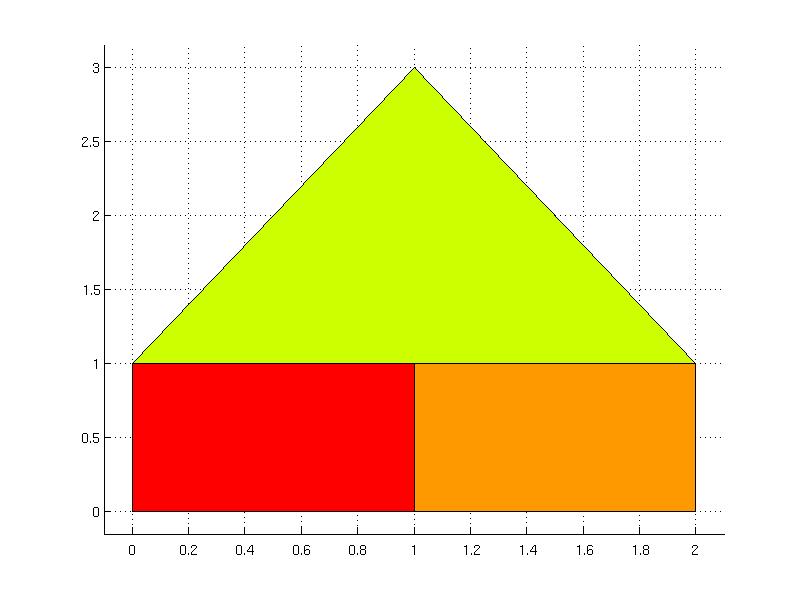
For instance, in the next example the union of polyhedra is build only from bounded polyhedra that are connected, not-overlapping and build a convex union

 P(1) = Polyhedron([0 0; 1 0; 1 1; 0 1]);
 P(2) = Polyhedron([1 0; 2 0; 2 1; 1 1]);
 P(3) = Polyhedron([0 1; 1 3; 2 1]);
 U = PolyUnion('Set', P, 'Bounded', true, 'Connected', true, 'Overlaps', false, 'Convex', true);

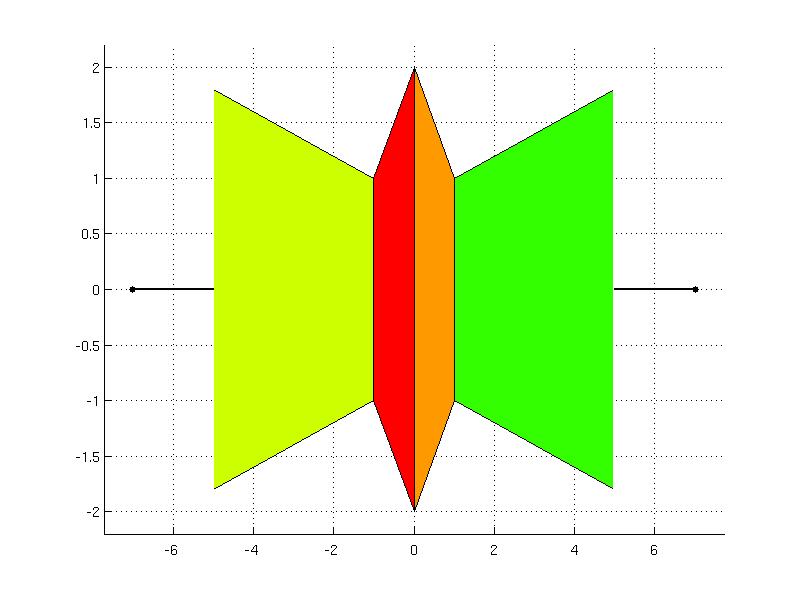
Example of a non-convex union:

 Q(1) = Polyhedron([0 -2; -1 -1; -1 1; 0 2]);
 Q(2) = Polyhedron([0 -2; 1 -1; 1 1; 0 2]);
 Q(3) = Polyhedron('V', [-1 -1; -1 1], 'R', [-1 0.2; -1 -0.2]);
 Q(4) = Polyhedron('V', [1 -1; 1 1], 'R', [1 0.2; 1 -0.2]);
 U = PolyUnion('Set', Q, 'Convex', false, 'Connected', true, 'Bounded', false);

If the properties of the union are not provided at the construction, the PolyUnion class contains methods for determining convexity, overlaps, connectivity, full-dimensionality and boundedness. Please note, that some of these methods are computationally expensive and the computation may be time consuming:

 U.isConvex()
 U.isOverlapping()
 U.isConnected()
 U.isFullDim()
 U.isBounded()

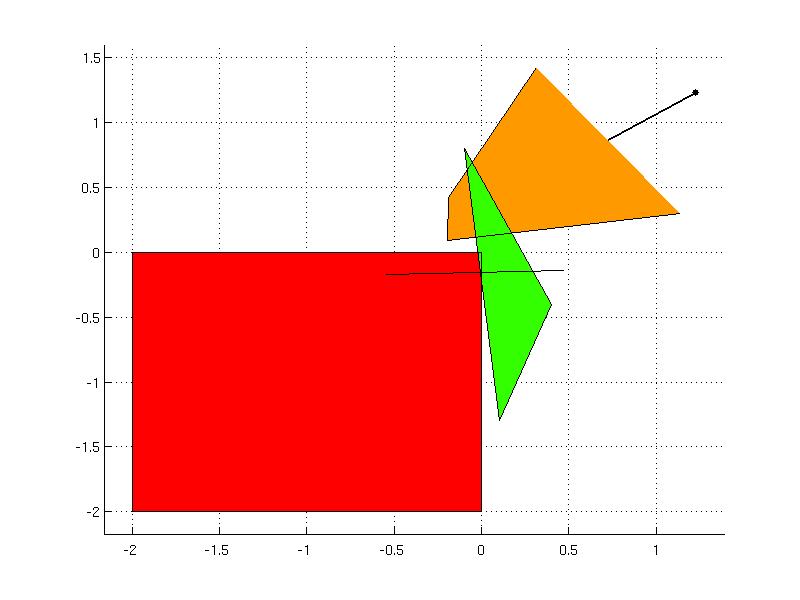
Consider the following example, which is constructed out of four polyhedra without specifying any properties. The convexity, overlaps, connectivity, full-dimensionality and boundedness properties of the union can be obtained as

 R(1) = Polyhedron('lb', [-2;-2], 'ub', [0; 0]);
 R(2) = Polyhedron('A', [-1 0.5; 0.4 -2.5; -7.5 0.2], 'b', [0.4; -0.3; 1.5]);
 R(3) = Polyhedron('A', [2.5 1.6; 0.3 -1.2; -0.8 -0.1; 0.7 -1.2; -2.3 -1.4; 0.3 0.3], 'b', [2.3; 4.2; 1.9; 0.5; 1.5; 0.8], 'Ae', [0.1 -3.2], 'be', 0.5 );
 R(4) = Polyhedron('V', [0.4 -0.4; -0.1 0.8; 0.1 -1.3]);
 U = PolyUnion(R)
 U.isFullDim()
 U.isBounded()
 U.isConnected()
 U.isConvex()
 U.isOverlapping()

Back to computational geometry overview.