Geometry /

Sets

Construction and properties of basic sets

High-level ConvexSet object

In MPT3 there are new classes of objects to represent convex sets that are derived from a common ConvexSet object. The ConvexSet object contains the information on the dimension of the set and it can store arbitrary user data. The dimension is available under Dim property and the user data can be stored in Data property. These properties are visible when typing

properties('ConvexSet')

The ConvexSet object cannot be constructed directly, it is higher level object for sharing common properties in convex sets. The properties are accessible in the objects derived from this class, such as Polyhedron and YSet.

The Polyhedron object - representation of polyhedra

The Polyhedron object represents a polyhedron given as the intersection of inequalities and equalities (referred to as H-representation)

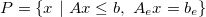
or as the convex combination of vertices and rays (referred to as V-representation)

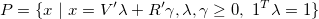
Both representations of polyhedra can be easily constructed in MPT3 providing the corresponding data. For instance, to construct the H-representation it suffices to provide the inequality and equality description in matrix form:

A = [2.7694   -1.3499;    3.0349    0.7254;   -0.0631    0.7147];
b = [0.5675;    1.6870;    3.6629];
Ae = [0.1246, -1.012];
be = 2.45;
P = Polyhedron('A', A, 'b', b, 'Ae', Ae, 'be', be);

The data are stored as they are provided, no automatic scaling or conversion is performed unless a given operation is performed on the polyhedron. The stored data can be retrieved in the appropriate fields A, b, Ae, be

P.A
P.b
P.Ae
P.be

The data can be extracted in a more compact form - using the properties H and He. The H property collects the matrices for inequality description H = [A, b] and the He property collects the matrices of equality description He = [Ae, be] :

P.H
P.He

The V-representation of the polyhedron can be constructed by providing a set of vertices and rays. Vertices are accepted in a matrix form stored row-wise (each row of a matrix corresponds to a vertex):

V = [-1.0  -0.8;  -2.9  1.4;  0.3  -0.7];
R = [-0.5, 1.9];
P = Polyhedron('V', V, 'R', R);

The data can be retrieved from the corresponding fields V and R:

P.V
P.R

The dimension of the polyhedral set is available in Dim property that is inherited from the higher level ConvexSet object

P.Dim

The user can store arbitrary data with the Polyhedron object with the help of Data property that is inherited from from ConvexSet object. As an example, consider that you want to store additional data that generated the V-representation. One possibility is to create a structure with the user data, e.g.

data.name = 'filename01.dat';
data.size = 5;
V = [1, -2; -1, 2; 3, 3];
P = Polyhedron('V', V, 'Data', data);

The user provided data are accessible in Data property and can be modified after construction of the object:

P.Data
P.Data.size = 6;

If the Polyhedron object exists, but it is not known which representation it has, it can be figured out using the following methods:

P.hasHRep
P.hasVRep

The output is a logical variable that indicates in which form is the polyhedron stored.

The polyhedron is in minimal (irredundant) H-representation, if the are no redundant inequalities/equalities describing the set. To query if the minimal representation of the polyhedron has been computed, one can use the following properties

P.irredundantHRep
P.irredundantVRep

that apply either for H- or V-representation. To compute the minimal H- or V-representation, one can employ the methods

P.minHRep()
P.minVRep()

As an example, consider the polyhedron build by two intervals -1 <= x <= 1, -2 <= x <= 2 . The first interval is completely contained in the second interval and to describe the set only the first interval is sufficient. We can check this by constructing the polyhedron from the inequality description

A = [-1; 1; -1; 1]; b = [1; 1; 2; 2];
P = Polyhedron('A', A, 'b', b);
P.irredundantHRep

One can see in the output that the minimal representation of the polyhedron has not been computed yet. Computing the minimal representation for the above example gives only the first interval which can be checked by calling

P.minHRep();
P.irredundantHRep
P.H

To quickly construct Polyhedron objects, one can resort to fast syntax that comprises only of inequalies or vertices. The fast syntax for inequality description is given as

A = [-1, 2, 0; -0.1, -3.1, 1.8]; b = [5.5; 3.8];
P = Polyhedron(A, b);

and for vertex description

V = [0, 1, -2; -1, 0.5 -4; 1, -1, 0.8; -4, -5, -0.9];
P = Polyhedron(V);

The YSet object - representation of general convex sets

The YSet object is an MPT interface to import convex sets described with the help of YALMIP. To construct the YSet object one needs to define the symbolic variables for representing the sets and consequently to create appropriate constraint sets using YALMIP. Consider an interval of the form -1 <= x <= 1 . In YALMIP this interval can be modeled as follows:

 x = sdpvar(1);
 interval = [ -1 <= x <= 1 ];

which is better described in "Constraints" part of Yalmip Wiki. After creating the constraint set, the YSet object can be constructed as follows

 Y = YSet(x, interval);

which requires two arguments: the symbolic variables and the constraint set. Optionally, one can provide a third argument that corresponds to yalmip option settings (e.g. to specify a particular solver).

To construct a polyhedral set in YALMIP can be achieved by providing the corresponding data. For instance, to create a H-representation can be achieved as

 x = sdpvar(2,1);
 A = [ -0.37,  0.81; 0.79,  0.12;  0.57,  0.41; -0.98,  0.75];
 b = [1; 2.3; 1.4; 2.8]
 constraints = [A*x <= b ];
 Y = YSet(x, constraints)

Note that the variables must be provided in as a vector. For instance, to model a set given by linear matrix inequality A*X + X*A' <= -I can be done as follows

 X = sdpvar(3);
 A = randn(3);
 constraints = [A*X + X*A' <= -eye(3) ];
 Y = YSet(X(:), constraints)

The input data for the YSet object can be retrieved by referring the appropriate properties

 Y.vars
 Y.constraints

Similarly as with the Polyhedron object, two properties are inherited from the ConvexSet class. In particular, the dimension of the set can be invoked using

 Y.Dim

and the user data stored with the set can be found under

 Y.Data

property. The Data property can be modified after the object has been created.

YALMIP allows creation of various sets, including cones that can be imported to MPT

x = sdpvar(2,1);
F = [cone(x(1),x(2)),  -1<= x <= 5];
Y = YSet(x, F)

Back to Computational Geometry overview.