OperationsWithPolyhedra
Geometry.OperationsWithPolyhedra History
Hide minor edits - Show changes to markup
For further help on the methods of the Polyhedron class, type help at the Matlab prompt. For instance, to obtain the help description for Minkowski summation in plus method, type
help Polyhedron/plus
or display the Matlab documentation that contains additional examples on the geometric methods
(:source lang=MATLAB -getcode:)mptdoc
and search for the specific method there.
plus- Minkowski summationminus- Pontryagin difference
affineHull- affine hullaffineMap- affine mapsinvAffineMap- inverse affine mapsgrid- regular grid of the polytopemeshGrid- grid given as coordinates for 2D polytopesmldivide- set differencenormalize- normalization of H-representationproject- project a point onto a setprojection- orthogonal projection onto axisslice- cuts of polyhedratriangulate- triangulationvolume- computing a volume
Computation of the Chebyshev center corresponds to inscribing a circle inside a polyhedron which is implemented in the chebyCenter method. The circle is described as {$ \{ x ~|~ \| x-x_c \|_2 \le r \} $} where {$x_c$} is the center and {$ r $} is the radius. Consider the following polyhedron
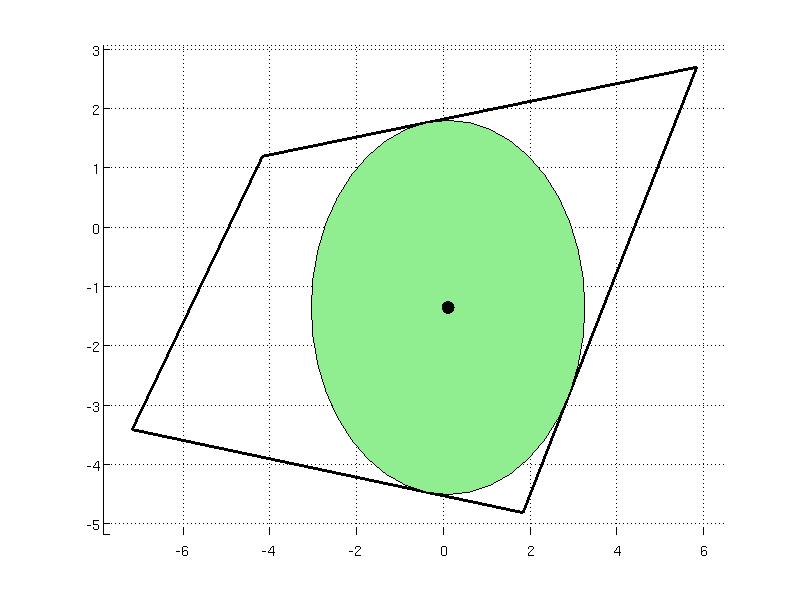
Computation of the Chebyshev center corresponds to inscribing the largest ball inside a polyhedron which is implemented in the chebyCenter method. The ball is described as {$ \{ x ~|~ \| x-x_c \|_2 \le r \} $} where {$x_c$} is the center of the ball and {$ r $} is the radius. Consider the following polyhedron
The data of the circle can be computed by calling
The data of the ball can be computed by calling
where the field x represents the center and r is the radius. The field exitflag is the status returned from the optimization solver. As the circle is a convex set, it can be represented as YSet object and plotted together with the polyhedron
where the field x represents the center and r is the radius. The field exitflag is the status returned from the optimization solver. As the ball is a convex set, it can be represented as YSet object and plotted together with the polyhedron
Computation of the Chebyshev center corresponds to inscribing a circle inside a polyhedron which is implemented in the chebyCenter method. The circle is described as {$ x | \| x-x_c \|_2 \le r $} where {$x_c$} is the center and {$ r $} is the radius. Consider the following polyhedron
Computation of the Chebyshev center corresponds to inscribing a circle inside a polyhedron which is implemented in the chebyCenter method. The circle is described as {$ \{ x ~|~ \| x-x_c \|_2 \le r \} $} where {$x_c$} is the center and {$ r $} is the radius. Consider the following polyhedron
Computation of the Chebyshev center corresponds to inscribing a circle inside a polyhedron which is implemented in the chebyCenter method. The circle is described as ${ x | \| x-x_c \|_2 \le r $} where {$x_c$} is the center and {$ r $} is the radius. Consider the following polyhedron
Computation of the Chebyshev center corresponds to inscribing a circle inside a polyhedron which is implemented in the chebyCenter method. The circle is described as {$ x | \| x-x_c \|_2 \le r $} where {$x_c$} is the center and {$ r $} is the radius. Consider the following polyhedron
To test wheter the polyhedron P contains the origin {$x_0 = [0; 0] $}, the function contains is invoked
To test wheter the polyhedron P contains the origin x0 = [0; 0] , the function contains is invoked
The answer is yes, so the point {$x_0$} is contained inside the polyhedron. What about the point {$x_1 = [3; 0] $}?
The answer is yes, so the point {$x_0$} is contained inside the polyhedron. What about the point x1 = [3; 0] ?
Computation of the Chebyshev center corresponds to inscribing a circle inside a polyhedron which is implemented in the chebyCenter method. The circle is described as ${ x | \| x-x_c \|_2 \le r $} where {$x_c$} is the center and {$ r $} is the radius. Consider the following polyhedron
P5 = Polyhedron([ 1.8 -4.8; -7.2 -3.4; -4.2 1.2; 5.8 2.7]);
The data of the circle can be computed by calling
(:source lang=MATLAB -getcode:)
data = P5.chebyCenter()
data =
exitflag: 1
x: [2x1 double]
r: 3.1497
where the field x represents the center and r is the radius. The field exitflag is the status returned from the optimization solver. As the circle is a convex set, it can be represented as YSet object and plotted together with the polyhedron
x = sdpvar(2,1);
S = YSet(x, norm(x - data.x) <= data.r);
P5.plot('wire', true, 'linewidth', 2);
hold on
S.plot('color', 'lightgreen');
plot(data.x(1), data.x(2), 'ko', 'MarkerSize', 10, 'MarkerFaceColor', 'k');
Note that conversion between H- and V-representations is numerically expensive and can become time-consuming for polyhedra with large number of facets or vertices. The numerical computation is delegated to an external CDD solver that should be present at the installation path. ( If not, type tbxmanager install cddmex to install it.)
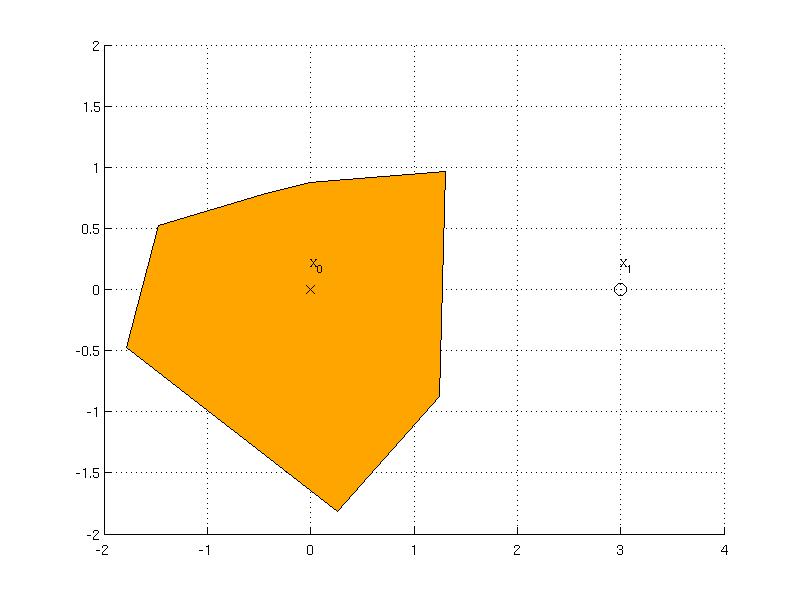
The Polyhedron class implements the contains method which tests whether a point (or a set of points) is contained inside a polyhedron. Consider the following polyhedron in V-representation
V = [ -1.7 -0.4; -0.4 0.7; 1.2 -0.8; 0 0.8; 1.3 0.9; -0.3 0.6]; P4 = Polyhedron(V);
To test wheter the polyhedron P contains the origin {$x_0 = [0; 0] $}, the function contains is invoked
x0 = [0; 0];
P4.contains( x0 )
ans =
1
The answer is yes, so the point {$x_0$} is contained inside the polyhedron. What about the point {$x_1 = [3; 0] $}?
(:source lang=MATLAB -getcode:)
x1 = [3; 0];
P4.contains( x1 )
ans =
0
The test containment for the points {$x_0$} and {$x_1$} is visualized in the figure below.
- H-representation
- H-representation (by inequalities and equalities)
- V-representation
- V-representation (by vertices and rays)
which can be converted vice-versa. The conversion from H- to V-representation is achieved via computeVRep method. Consider the following polyhedron which is created in H-representation
P2 = Polyhedron('lb', [-1; -2], 'ub', [3; 4])
Polyhedron in R^2 with representations:
H-rep (redundant) : Inequalities 4 | Equalities 0
V-rep : Unknown (call computeVRep() to compute)
Functions : none
P2.hasVRep
ans =
0
To compute the V-representation, the method computeVRep method is called
P2.computeVRep
Polyhedron in R^2 with representations:
H-rep (redundant) : Inequalities 4 | Equalities 0
V-rep (redundant) : Vertices 4 | Rays 0
Functions : none
To obtain the vertices and rays, one has to refer to V and R properties
P2.V
ans =
3 -2
-1 -2
-1 4
3 4
P2.R
ans =
Empty matrix: 0-by-2
Note that the method computeVRep is executed automatically when queried for vertices or rays using V or R properties.
The conversion from V- to H-representation is achieved via computeHRep method. Consider the following triangle
P3 = Polyhedron([4, -1; 4, 5; 8, 3])
Polyhedron in R^2 with representations:
H-rep : Unknown (call computeHRep() to compute)
V-rep (redundant) : Vertices 3 | Rays 0
Functions : none
P3.hasHRep
ans =
0
that comprises of three vertices. The H-representation can be computed by
(:source lang=MATLAB -getcode:)
P3.computeHRep
Polyhedron in R^2 with representations:
H-rep (redundant) : Inequalities 3 | Equalities 0
V-rep (redundant) : Vertices 3 | Rays 0
Functions : none
and the facets can be extracted by pointing to H, He properties (or A, Ae, b, be)
P3.H
ans =
1.0000 2.0000 14.0000
-1.0000 0 -4.0000
1.0000 -1.0000 5.0000
P3.He
ans =
Empty matrix: 0-by-3
When queried for facets, the method computeHRep is executed automatically.
help IterableBehavior
help Polyhedron/forEach
Polyhedra in the array can be removed
(:source lang=MATLAB -getcode:)row_array1(2) = []
The basic methods operate onto arrays
(:source lang=MATLAB -getcode:)
row_array2.isEmptySet
ans =
0 0
column_array1.isFullDim
ans =
1
1
column_array2.isBounded
ans =
1
1
If the method cannot be executed on an array, the forEach function can be applied. For instance, to compute the grid function cannot be evaluated on an array and one observes an error
row_array2.grid(5) Error using ConvexSet/grid (line 22) This method does not support arrays. Use the forEach() method.
In this case, the forEach method can be applied that executes the function on each polyhedron in the array. For more help on forEach function type
help IterableBehavior
The correct syntax for the above example using grid function is given as
N = 5; output = row_array2.forEach(@(x) grid(x, N), 'UniformOutput', false)
To create a new copy of a Polyhedron object, or an array of polyhedra, the method copy must be invoked otherwise the new object point to the same data, i.e.
Qnew = Q.copy()
Polyhedra can be grouped into column or row arrays. For this purpose in MPT there exist overloaded horzcat and vertcat operators or [ ] brackets. Consider the two following polyhedra
Q = Polyhedron('V', [1, -1; 0, -4; 2.5 -3]);
R = Polyhedron('V', [2.5, -3; -1, 4; 1, -1; -1, 2]);
The row array of polyhedra Q, R can be created twofold
row_array1 = [Q, R] row_array2 = horzcat(Q, R)
Similarly, the column array is created as
(:source lang=MATLAB -getcode:)column_array1 = [Q; R] column_array2 = vertcat(Q, R)
Each polyhedron in the array can be extracted using indices, e.g.
(:source lang=MATLAB -getcode:)row_array1(1) column_array1(2)
P1.isEmptySet
P1.isEmptySet()
P1.isFullDim
P1.isFullDim()
P1.isBounded
P1.isBounded()
P1.plot()
The Polyhedron object can be created in two forms
- H-representation
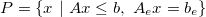
- V-representation
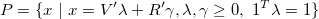
The Polyhedron class contains methods that are very useful for determining the basic properties such as
- emptyness -
isEmptySet - boundedness -
isBounded - full-dimensionality -
isFullDim
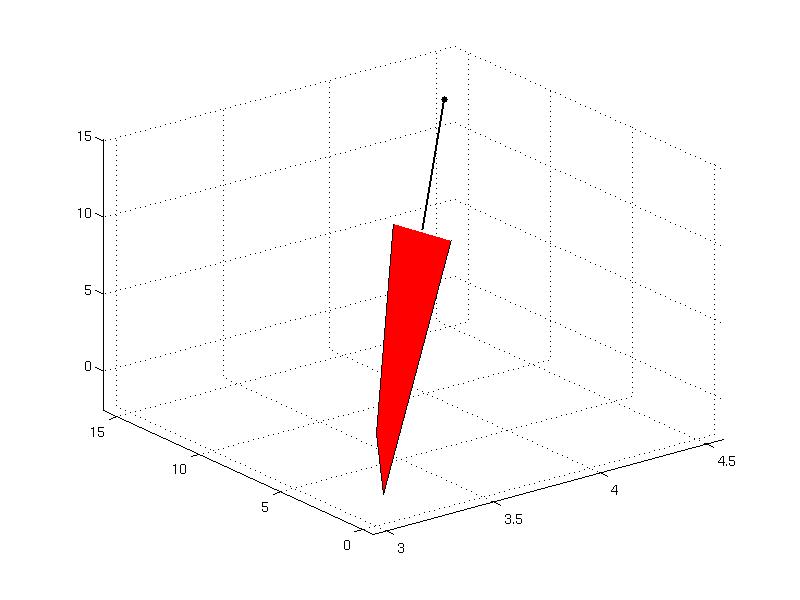
As an example, consider the lower-dimensional polyhedron in the dimension 3
(:source lang=MATLAB -getcode:)P1 = Polyhedron( 'A', [1 -2.1 -0.5; 0.8 -3.1 0.9; -1.2 0.4 -0.8], 'b', [1; 4.9; -1.8], 'Ae', [1 -0.1 0], 'be', 3)
To query, if the set is empty or nor, use
(:source lang=MATLAB -getcode:)
P1.isEmptySet
ans =
0
From the construction it is evident that the polyhedron is lower-dimensional because it contains one equality constraint. This fact can be checked using the method
(:source lang=MATLAB -getcode:)
P1.isFullDim
ans =
0
Boundedness property can be queried by
(:source lang=MATLAB -getcode:)
P1.isBounded
ans =
0
method. One can plot the polyhedron to verify that the above properties are true
Facet and vertex enumeration
The Polyhedron object can be created in two forms
- H-representation
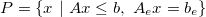
- V-representation
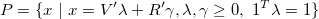
Chebyshev center
Chebyshev center
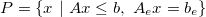
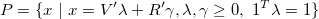
The Polyhedron object can be created in two forms
- H-representation
- V-representation
Back to computational geometry overview.
Methods for determining basic properties
Working with multiple polyhedra
Geometric methods
Set containment
Chebyshev center
Back to Computational Geometry overview.
Geometric operations with polyhedra
Back to computational geometry overview.